з”ЁGTOжқҘдәҶи§Јеҫ·е·һжү‘е…Ӣдёӯд»Җд№ҲжҳҜйҡҗжҷҰиө”зҺҮпјҹ
2025-12-29 | еҲҶзұ»:GTOзӯ–з•Ҙ/GTOиҪҜ件 | иҜ„и®ә:0дәә | жөҸи§Ҳ:185ж¬Ў
- жӯЈж–ҮеҶ…е®№
- жҲ‘жқҘиҜҙдёӨеҸҘ:(е·Іжңү0дәәеҸӮдёҺпјү
йҡҗеҗ«иө”зҺҮжҳҜжү‘е…ӢзҗҶи®әдёӯзҡ„дёҖдёӘе…ій”®жҢҮж ҮгҖӮдҪ еҸҜиғҪеҗ¬иҜҙиҝҮиҝҷдёӘжңҜиҜӯпјҢ并且еҜ№е®ғзҡ„жҰӮеҝөжңүдәҶдёҖдәӣеҹәжң¬зҡ„дәҶи§ЈпјҢдҪҶжҳҜпјҢеңЁжұӮи§ЈеҷЁж—¶д»ЈпјҢиҝҷдёӘжҰӮеҝөе·Із»ҸеҸ‘з”ҹдәҶеҫҲеӨ§зҡ„еҸҳеҢ–гҖӮ
д»Җд№ҲжҳҜйҡҗеҗ«иө”зҺҮпјҹ
йҡҗеҗ«иө”зҺҮжҳҜжҢҮдҪ йў„жңҹиҺ·еҫ—зҡ„收зӣҠпјҢи¶…иҝҮдҪ иҮӘиә«зүҢеҠӣжүҖеҜ№еә”зҡ„д»·еҖјгҖӮдҪ еҸҜд»ҘжҠҠе®ғзҗҶи§ЈдёәпјҢеҪ“дҪ зҡ„зүҢеҠӣи¶…иҝҮеҜ№жүӢж—¶пјҢдҪ йў„жңҹеңЁжңӘжқҘеҮ иҪ®дёӯиҺ·еҫ—зҡ„收зӣҠгҖӮиҝҷдёӘжҰӮеҝөдёҺвҖңзӣҙжҺҘеә•жұ иө”зҺҮвҖқеҪўжҲҗеҜ№жҜ”пјҢз”ЁжқҘи§ЈйҮҠдёәд»Җд№ҲжңүдәӣзүҢеҚідҪҝзүҢеҠӣдёҚи¶ід»Ҙи·ҹжіЁпјҢд№ҹиғҪйҖҡиҝҮи·ҹжіЁиҺ·еҲ©гҖӮ
зӣҙжҺҘиө”зҺҮдёҺйҡҗеҗ«иө”зҺҮ
дёҫдёӘдҫӢеӯҗгҖӮиҪ¬зүҢеңҲжҲ‘们йқўдёҙдёҖдёӘ10BBзҡ„еә•жұ еӨ§е°Ҹзҡ„дёӢжіЁгҖӮжҲ‘们жҢҒжңүиғңзҺҮдёә25%зҡ„еҗ¬зүҢгҖӮжҲ‘们еә”иҜҘи·ҹжіЁеҗ—пјҹ
зӣҙжҺҘеә•жұ иө”зҺҮи®Ўз®—
зӣҙжҺҘеә•жұ иө”зҺҮжҢҮзҡ„жҳҜпјҢдёәдәҶиҮіе°‘收еӣһжҲҗжң¬пјҢдҪ йңҖиҰҒиөўеӨҡе°‘зҷҫеҲҶжҜ”зҡ„иөҢжіЁгҖӮиҝҷйҮҢеҒҮи®ҫд№ӢеҗҺжІЎжңүиҝҪеҠ иө„йҮ‘гҖӮ
- жңү 25% зҡ„жҰӮзҺҮжҲ‘们еҮ»дёӯзӣ®ж ҮзүҢеһӢ并иөўеҫ— 20BBпјҲеә•жұ + еҜ№жүӢзҡ„дёӢжіЁпјүгҖӮ
- 75% зҡ„жғ…еҶөдёӢжҲ‘们дјҡеӨұеҲ©пјҢжҚҹеӨұ 10 дёӘеӨ§зӣІжіЁпјҲжҲ‘们зҡ„йў„жөӢпјүгҖӮ
и®Өиҙӯзҡ„йў„жңҹд»·еҖј = (25% x 20BB) вҖ“ (75% x 10BB) = 5 вҖ“ 7.5 = -2.5BB
жҳҫ然пјҢиҝҷжҳҜдёӘдәҸжң¬зҡ„иөҢжіЁгҖӮ然иҖҢпјҢиҝҷз§Қи®Ўз®—ж–№жі•зҡ„й—®йўҳеңЁдәҺе®ғеҝҪз•ҘдәҶд№ӢеҗҺжҠ•е…Ҙеә•жұ зҡ„иө„йҮ‘вҖ”вҖ”иҖҢиҝҷжӯЈжҳҜйҡҗеҗ«иө”зҺҮеҸ‘жҢҘдҪңз”Ёзҡ„ең°ж–№пјҒ
йҡҗеҗ«иө”зҺҮи®Ўз®—
дёәдәҶиҜҒжҳҺиҝҷжӯҘи·ҹжіЁзҡ„еҗҲзҗҶжҖ§пјҢжҲ‘们йңҖиҰҒеңЁжІізүҢеңҲиөўдёҖдәӣйўқеӨ–зҡ„зӯ№з ҒпјҲMпјүгҖӮеҰӮжһңжІЎиөўпјҢжҲ‘们йҡҸж—¶еҸҜд»ҘејғзүҢгҖӮ
- жңү 25% зҡ„жҰӮзҺҮжҲ‘们еҮ»дёӯзӣ®ж ҮзүҢеһӢпјҢиөўеҫ— 20BB + MпјҲеә•жұ + еҜ№жүӢзҡ„дёӢжіЁ + MпјүгҖӮ
- 75% зҡ„жғ…еҶөдёӢжҲ‘们дјҡеӨұеҲ©пјҢжҚҹеӨұ 10 дёӘеӨ§зӣІжіЁпјҲжҲ‘们зҡ„йў„жөӢпјүгҖӮ
и°ғз”Ёйў„жңҹеҖј = (25% x (20+M)) вҖ“ (75% x 10)
дёәдәҶиҫҫеҲ°зӣҲдәҸе№іиЎЎпјҢжҲ‘们йңҖиҰҒеңЁе№іеұҖж—¶йўқеӨ–иөўеӨҡе°‘пјҹе°ҶжңҹжңӣеҖји®ҫдёәйӣ¶д»ҘжүҫеҲ°зӣҲдәҸе№іиЎЎзӮ№пјҢ然еҗҺжұӮи§Ј Mпјҡ
0 = (25% x (20+M)) вҖ“ (75% x 10)
M = 10
е№іеқҮиҖҢиЁҖпјҢжҲ‘们йңҖиҰҒеңЁжІізүҢеңҲеӨҡиөў10дёӘеӨ§зӣІжіЁжүҚиғҪиҜҒжҳҺи·ҹжіЁжҳҜеҗҲзҗҶзҡ„гҖӮиҝҷзӣёеҪ“дәҺеңЁжІізүҢеңҲдёӢжіЁдёүеҲҶд№ӢдёҖеә•жұ гҖӮжүҖд»ҘпјҢеҰӮжһңжҲ‘们и®ӨдёәеңЁеҮ»дёӯеҗ¬зүҢеҗҺиҮіе°‘иғҪиөўеҲ°дёүеҲҶд№ӢдёҖеә•жұ пјҢйӮЈд№Ҳиҝҷж¬Ўи·ҹжіЁе°ұжңүеҲ©еҸҜеӣҫдәҶпјҒ
жҚўеҸҘиҜқиҜҙпјҢи·ҹжіЁвҖңж„Ҹе‘ізқҖвҖқе®ғеңЁжІізүҢеңҲиҮіе°‘иғҪиөўеҲ°10дёӘеӨ§зӣІжіЁгҖӮиҝҷе°ұжҳҜиҝҷдёӘжңҜиҜӯеҗҚз§°зҡ„з”ұжқҘгҖӮ
е®ғдёҺиӮЎжқғе®һзҺ°зҡ„е…ізі»
е°ҸзӣІдҪҚејҖеұҖпјҢеӨ§зӣІдҪҚи·ҹжіЁгҖӮзҝ»зүҢдёәJвҷҘ TвҷҰ 6вҷҘгҖӮе°ҸзӣІдҪҚдёӢжіЁ 75%пјҢеӨ§зӣІдҪҚи·ҹжіЁгҖӮиҪ¬зүҢдёә2вҷЈгҖӮе°ҸзӣІдҪҚи¶…жіЁ 175%пјҢеӨ§зӣІдҪҚжүӢжҢҒ5вҷҘ3вҷҘиЎҢеҠЁгҖӮ
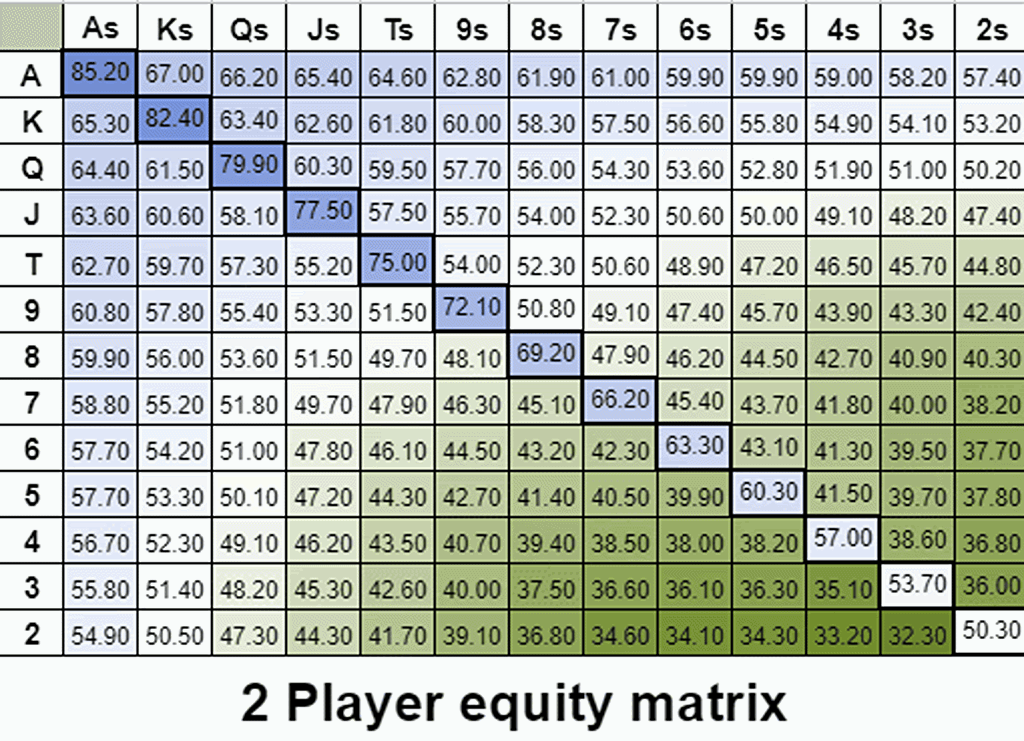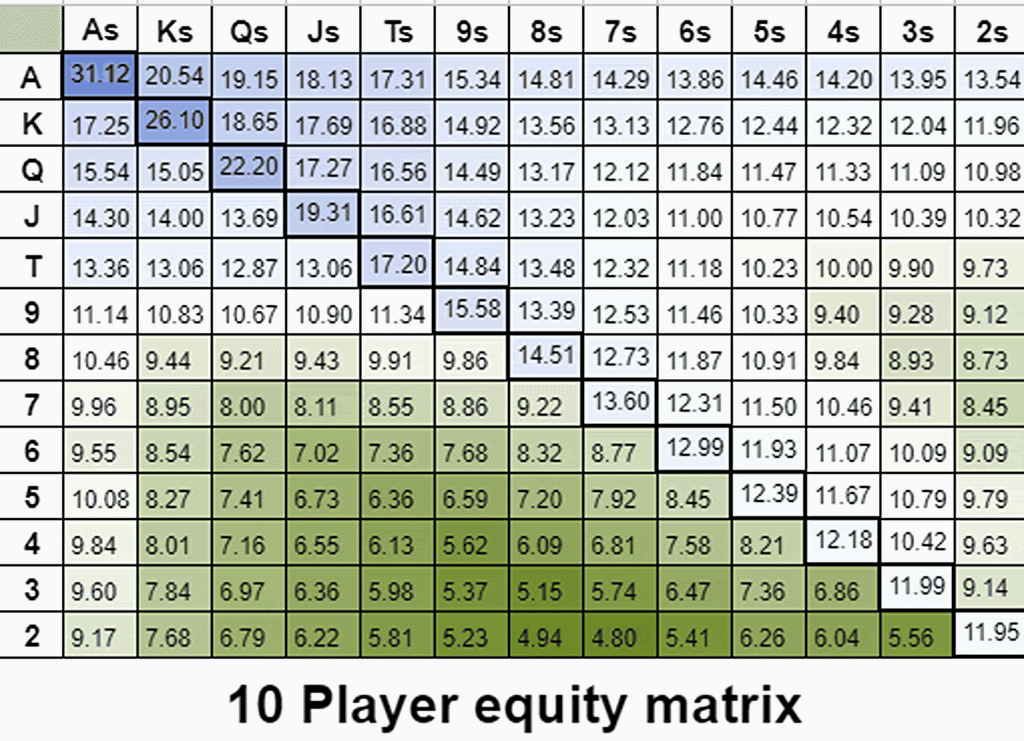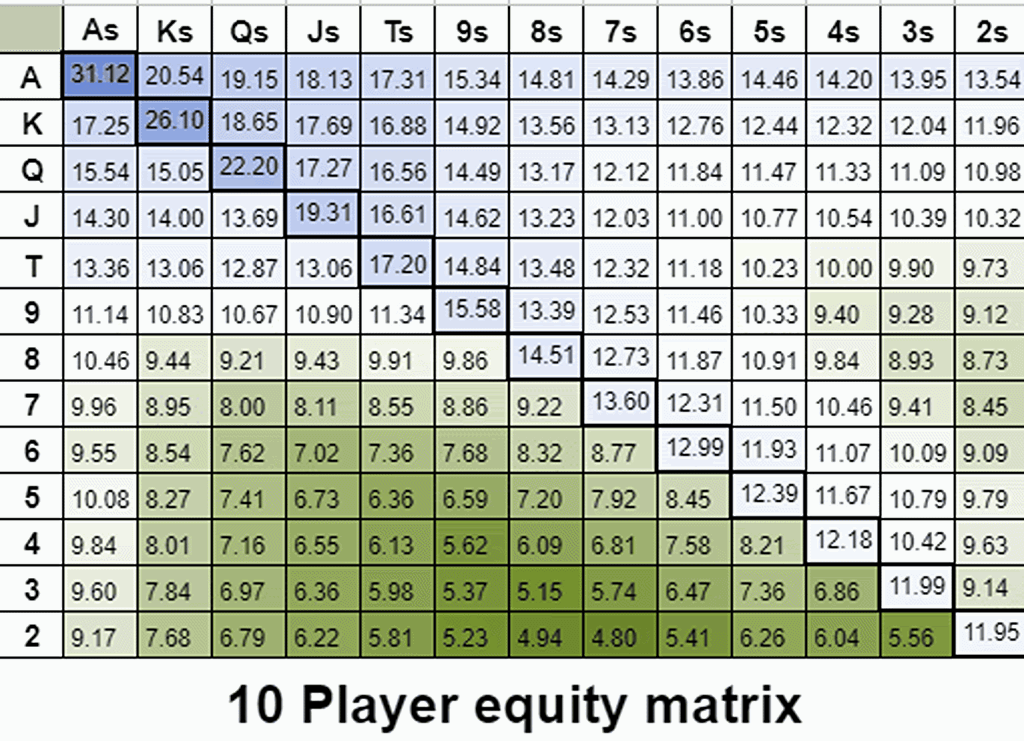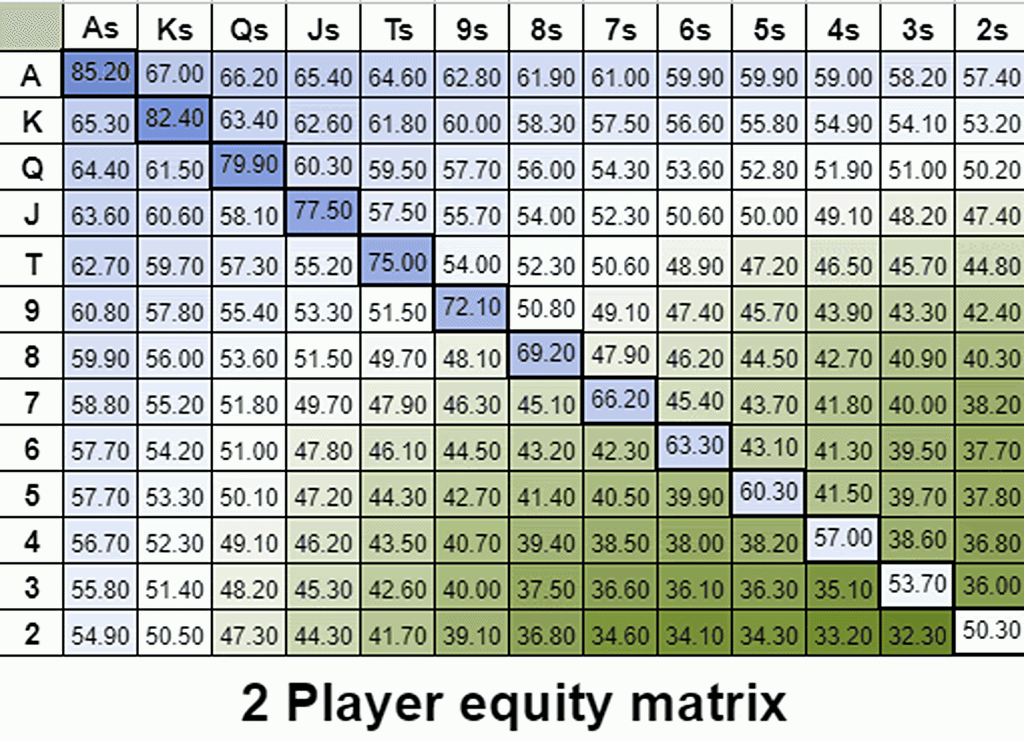
жҲ‘们е…ҲжқҘи®Ўз®—дёҖдёӢеә•жұ иө”зҺҮгҖӮеҒҮи®ҫжҲ‘们пјҲBBпјүйқўдёҙдёҖдёӘ26.25BBзҡ„дёӢжіЁпјҢеә•жұ жҳҜ15BBгҖӮдёәдәҶеңЁи·ҹжіЁдёӯдҝқжҢҒзӣҲдәҸе№іиЎЎпјҢд»Һй•ҝиҝңжқҘзңӢпјҢжҲ‘们иҮіе°‘йңҖиҰҒиөў26.25BBгҖӮ
еҒҮи®ҫжҲ‘们жүӢжҢҒдёҖжүӢиҫ№зјҳз»„еҗҲеҗ¬зүҢпјҢдҫӢеҰӮ5вҷҘ3вҷҘпјҢиғңзҺҮеҸӘжңү 31.68%гҖӮ
и®©жҲ‘们жқҘзңӢдёҖдёӢзӣҙжҺҘеә•жұ иө”зҺҮгҖӮжүҖйңҖиғңзҺҮ = пјҲи·ҹжіЁйҮ‘йўқпјү/пјҲи·ҹжіЁеҗҺзҡ„еә•жұ – жҠҪж°ҙпјүгҖӮеӨ§зӣІжіЁйңҖиҰҒ 26.25 / (15 + 26.25*2 – 0.6) = 39.24% зҡ„иғңзҺҮжүҚиғҪи·ҹжіЁгҖӮ
еҰӮжһңе°ҸзӣІдҪҚе…ЁжҠјпјҲжҲ–иҖ…жІізүҢеңҲжҖ»жҳҜиҝҮзүҢпјүпјҢиҝҷжүӢзүҢеҫҲе®№жҳ“ејғзүҢгҖӮ然иҖҢпјҢи·ҹжіЁеҗҺпјҢеҜ№жүӢд»Қ然жңү 66.25 дёӘеӨ§зӣІжіЁгҖӮ5h3h йў„и®ЎпјҢз”ұдәҺйҡҗеҗ«иө”зҺҮпјҢеҪ“е®ғеҮ»дёӯеҗ¬зүҢж—¶пјҢдјҡиөўеҫ—иҝңи¶…е…¶еә”еҫ—зҡ„зӯ№з ҒгҖӮ
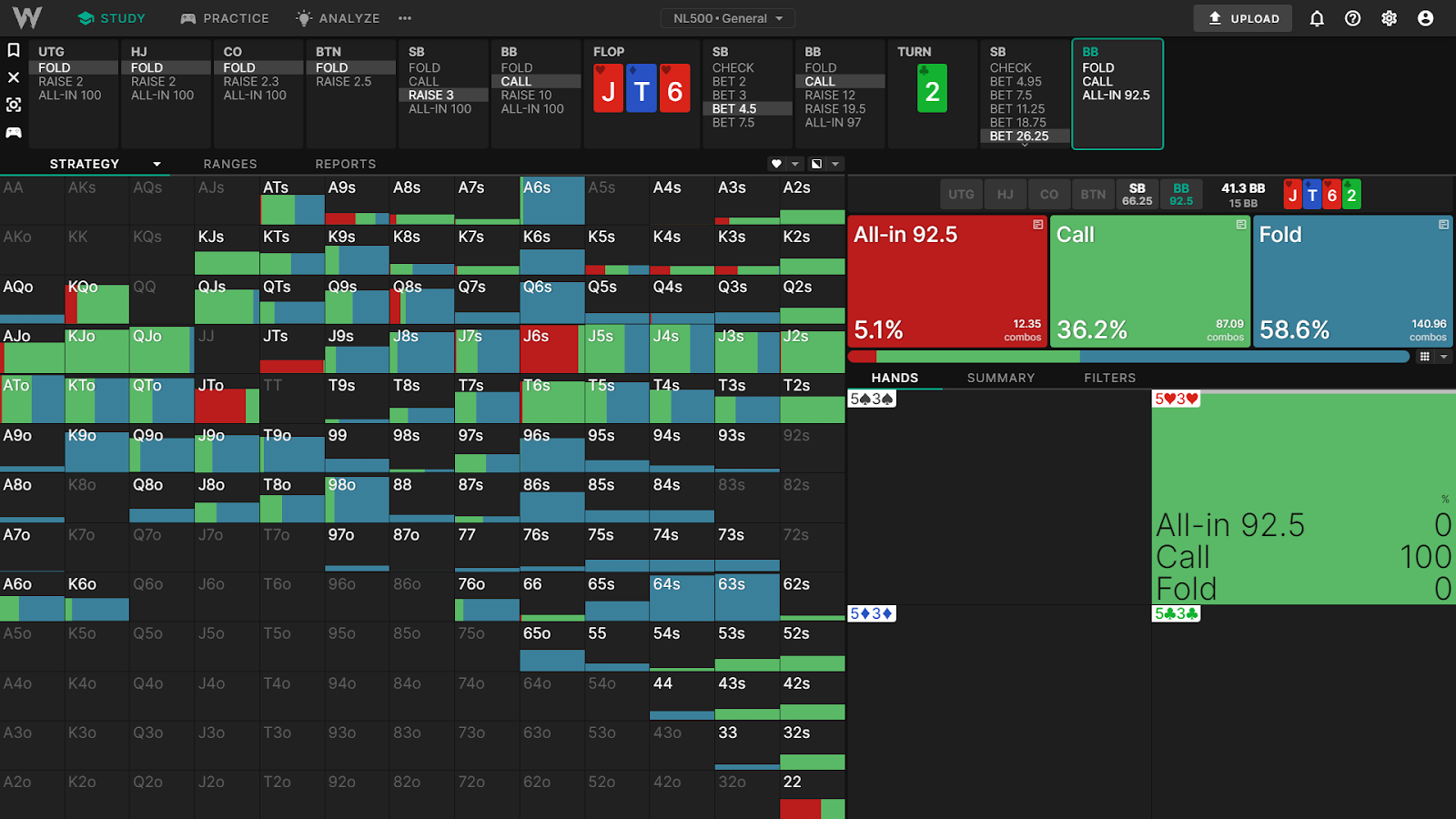
жҲ‘们用5h3hзҡ„жңҹжңӣеҖјжҜ”ејғзүҢй«ҳ5.33BBгҖӮиҝҷж„Ҹе‘ізқҖпјҢи·ҹжіЁеҗҺжҲ‘们预жңҹиғҪиөў(26.25BB + 5.33BB = 31.58BB)гҖӮи·ҹжіЁеҗҺеә•жұ дёә67.5BBпјҢеӣ жӯӨжҲ‘们预жңҹзҡ„еә•жұ д»Ҫйўқдёә(31.58 / 67.5) = 46.78%пјҲдёҚи®ЎжҠҪж°ҙпјүгҖӮ


и®©жҲ‘们еӣһйЎҫдёҖдёӢпјҡ
- жҲ‘们зҡ„еҺҹе§ӢжқғзӣҠдёә 31.68%гҖӮ
- жҲ‘们зҡ„д»ҪйўқжҳҜ46.78%гҖӮ
жҚўеҸҘиҜқиҜҙпјҢжҲ‘们超йўқе®һзҺ°дәҶжқғзӣҠпјҡ46.78/31.68 = 148%
жӣҙеҮҶзЎ®ең°иҜҙпјҢжҲ‘们зҡ„йў„жңҹд»·еҖјй«ҳдәҺжҲ‘们еҺҹе§ӢжқғзӣҠжүҖйҡҗеҗ«зҡ„д»·еҖјпјҢеӣ дёәжҲ‘们жңүиғҪеҠӣеңЁеҗҺжңҹиҺ·еҫ—и¶…йўқ收зӣҠгҖӮиҝҷе°ұжҳҜйҡҗеҗ«иө”зҺҮзҡ„еҹәжң¬жҖ§иҙЁгҖӮ
еҸҚеҗ‘йҡҗеҗ«иө”зҺҮ
еҸҚеҗ‘йҡҗеҗ«иө”зҺҮд№ҹеӯҳеңЁгҖӮдҫӢеҰӮпјҢжңүж—¶дҪ еҮ»дёӯдәҶеҗ¬зүҢпјҢеҚҙд»Қ然иҫ“жҺүдәҶдёҖеӨ§з¬”еә•жұ гҖӮжңүж—¶пјҢдёҖжүӢжҲҗзүҢеҚҙеӣ дёәеңЁеҗҺз»ӯеӣһеҗҲдёӯиў«еҜ№жүӢеҺӢеҲ¶жҲ–еҗ¬зүҢеӨұиҙҘиҖҢж— жі•иөўеҫ—еә”еҫ—зҡ„еә•жұ д»ҪйўқгҖӮеҚідҪҝеҸӘжӢҝеҲ°з¬¬дәҢеҘҪзҡ„ејәзүҢпјҢд№ҹеҸҜиғҪдёҘйҮҚеҪұе“ҚдҪ зҡ„зӣҲеҲ©гҖӮ
и®©жҲ‘们еӣһеҲ°жңҖеҲқзҡ„JвҷҘ TвҷҰ 6вҷҘ 2вҷЈдҫӢеӯҗпјҢеҒҮи®ҫжҲ‘们жҢҒжңүKвҷ Jвҷ гҖӮ


Kвҷ Jвҷ зүҢеһӢдёҚй”ҷпјҢиғңиҝҮеҜ№жүӢдёҖеҚҠд»ҘдёҠзҡ„зүҢеһӢиҢғеӣҙгҖӮ然иҖҢпјҢйқўеҜ№еҜ№жүӢзҡ„и¶…йўқдёӢжіЁпјҢе®ғеҮ д№ҺеҸӘиғҪеӢүејәиҫҫеҲ°зӣҲдәҸе№іиЎЎгҖӮеҪ“еҜ№жүӢзҡ„зүҢеһӢдёӨжһҒеҲҶеҢ–ж—¶пјҢдҪ йӮЈдәӣиҫ№зјҳжҲҗзүҢеҫҲйҡҫиғңиҝҮеҜ№жүӢзҡ„д»·еҖјзүҢгҖӮиҝҷдәӣзүҢжӣҙеғҸжҳҜжҠ“иҜҲ唬зүҢпјҢеҸҚеҗ‘йҡҗеҗ«иө”зҺҮеҫҲе·®гҖӮ
еҗҢж ·пјҢжҲ‘们йңҖиҰҒиөў 26.25BB жүҚиғҪиҫҫеҲ°зӣҲдәҸе№іиЎЎпјҢиҖҢKвҷ Jвҷ иөўдәҶ 26.25 + 2.21 = 28.46BBпјҢжҲ–еӨ§зәҰ 28.46/67.5 = еә•жұ зҡ„ 42%гҖӮ
еҺҹе§ӢжқғзӣҠпјҡ54.71%
дјҒдёҡд»·еҖјпјҡ42.16%
жқғзӣҠе®һзҺ°зҺҮ = 77%гҖӮ
жҚўеҸҘиҜқиҜҙпјҢжҲ‘们еҸӘе®һзҺ°дәҶ77%зҡ„еҺҹе§ӢжқғзӣҠгҖӮ
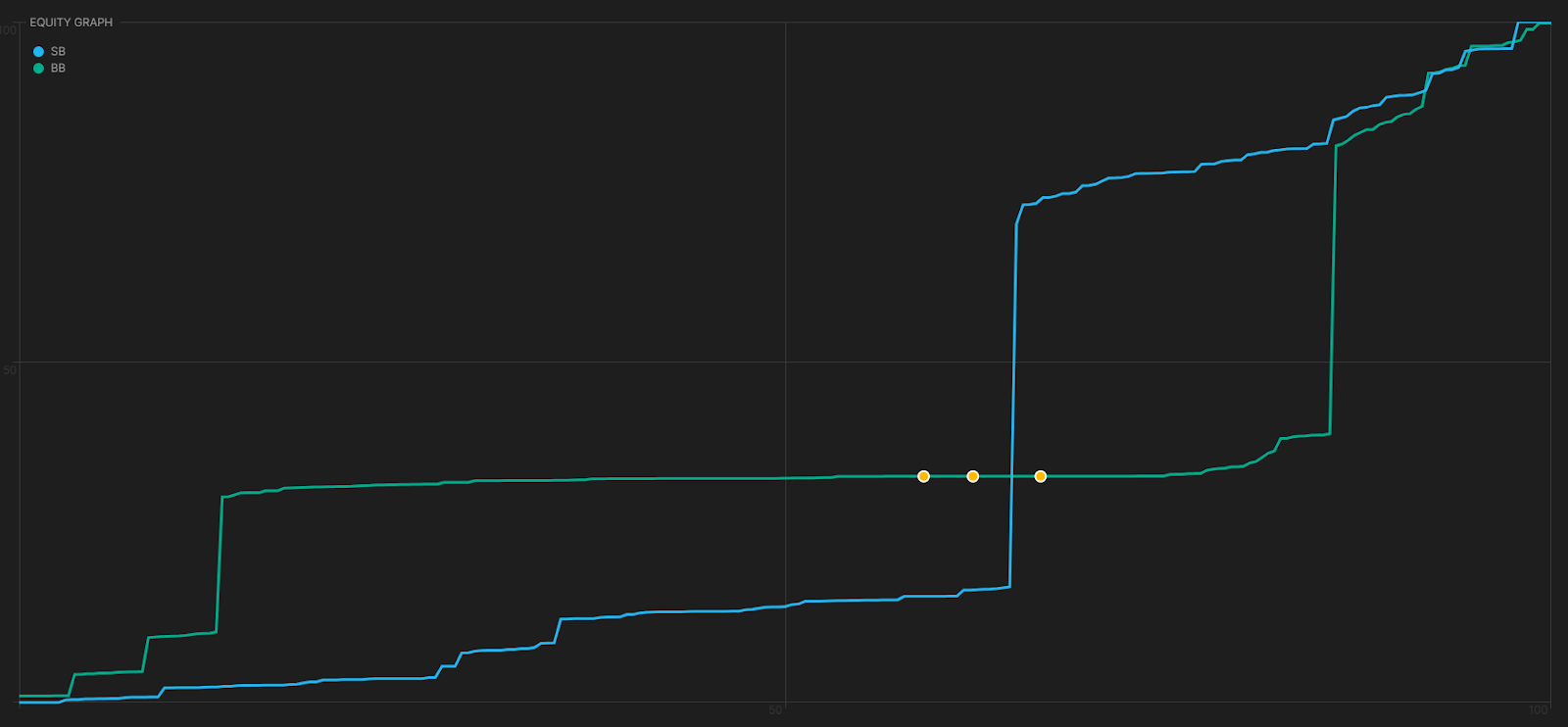
йӮЈд№ҲжҲ‘们еү©дёӢзҡ„жңҹжңӣеҖјйғҪеҺ»е“Әе„ҝдәҶе‘ўпјҹе°ҸзӣІжіЁжңүиғҪеҠӣи¶…йўқе®һзҺ°д»–们зҡ„жқғзӣҠпјҢи®©жҲ‘们зҡ„йЎ¶еҜ№еңЁжІізүҢеңҲйҷ·е…ҘеҫҲеӨҡж— е…ізҙ§иҰҒзҡ„еұҖйқўгҖӮ他们еҸҜд»Ҙз”Ёжӣҙејәзҡ„д»·еҖј/иҜҲ唬жқҘеҺӢеҲ¶жҲ‘们пјҢиғңиҝҮжҲ‘们пјҢ然еҗҺиөўдёӢжҲ‘们зҡ„йЎ¶еҜ№пјҢд»ҺиҖҢиҺ·еҫ—е·ЁйўқеҲ©ж¶ҰгҖӮжҲ‘们дёҚеҸҜиғҪи·ҹжіЁжІізүҢеңҲзҡ„жҜҸдёҖжіЁгҖӮжҲ‘们жңүдёҖдёӘдё“й—ЁжҠ“иҜҲ唬зҡ„зүҢжүӢпјҢдҪҶз”ұдәҺ他们зҡ„иҢғеӣҙеӨӘејәпјҢеҚідҪҝзүҢеҠӣжӣҙејұпјҢд№ҹж— жі•д»ҺдёӯжҰЁеҸ–д»·еҖјгҖӮ
и®©жҲ‘们用еӣҫиЎЁжқҘеұ•зӨәдёҖдёӢгҖӮиҝҷжҳҜйқўеҜ№еҜ№ж–№и¶…йўқдёӢжіЁж—¶жҲ‘们зҡ„жқғзӣҠеҲҶеёғгҖӮзәҝдёҠзҡ„зӮ№д»ЈиЎЁжҲ‘们жүҖжңүзҡ„KJгҖӮжӯЈеҰӮдҪ жүҖзңӢеҲ°зҡ„пјҢеӨ§зӣІжіЁзҡ„еӨ§йғЁеҲҶзүҢеһӢиҢғеӣҙйғҪжҜ”иҫғдёӯз«ӢпјҢиҝҷеҸҜд»Ҙд»ҺйӮЈжқЎй•ҝй•ҝзҡ„гҖҒе№іеқҰзҡ„жҠ“иҜҲ唬зүҢеһӢзәҝзңӢеҮәгҖӮ
йҡҗеҗ«иө”зҺҮдёҺзӯ№з Ғж·ұеәҰзҡ„е…ізі»
зӯ№з Ғж·ұеәҰжҳҜиҜ„дј°йҡҗеҗ«иө”зҺҮж—¶жңҖйҮҚиҰҒзҡ„еӣ зҙ гҖӮиҜ·и®°дҪҸпјҢвҖңйҡҗеҗ«вҖқжҢҮзҡ„жҳҜжҲ‘们预жңҹеңЁеҗҺз»ӯеӣһеҗҲдёӯиөўеҫ—жӣҙеӨҡзӯ№з ҒгҖӮжҲ‘们жӢҘжңүзҡ„зӯ№з Ғи¶ҠеӨҡпјҢеңЁеҗҺз»ӯеӣһеҗҲдёӯиөўеҫ—пјҲжҲ–иҫ“жҺүпјүзӯ№з Ғзҡ„еҸҜиғҪжҖ§е°ұи¶ҠеӨ§пјҢйҡҗеҗ«иө”зҺҮ/еҸҚеҗ‘йҡҗеҗ«иө”зҺҮд№ҹе°ұи¶Ҡй«ҳгҖӮ
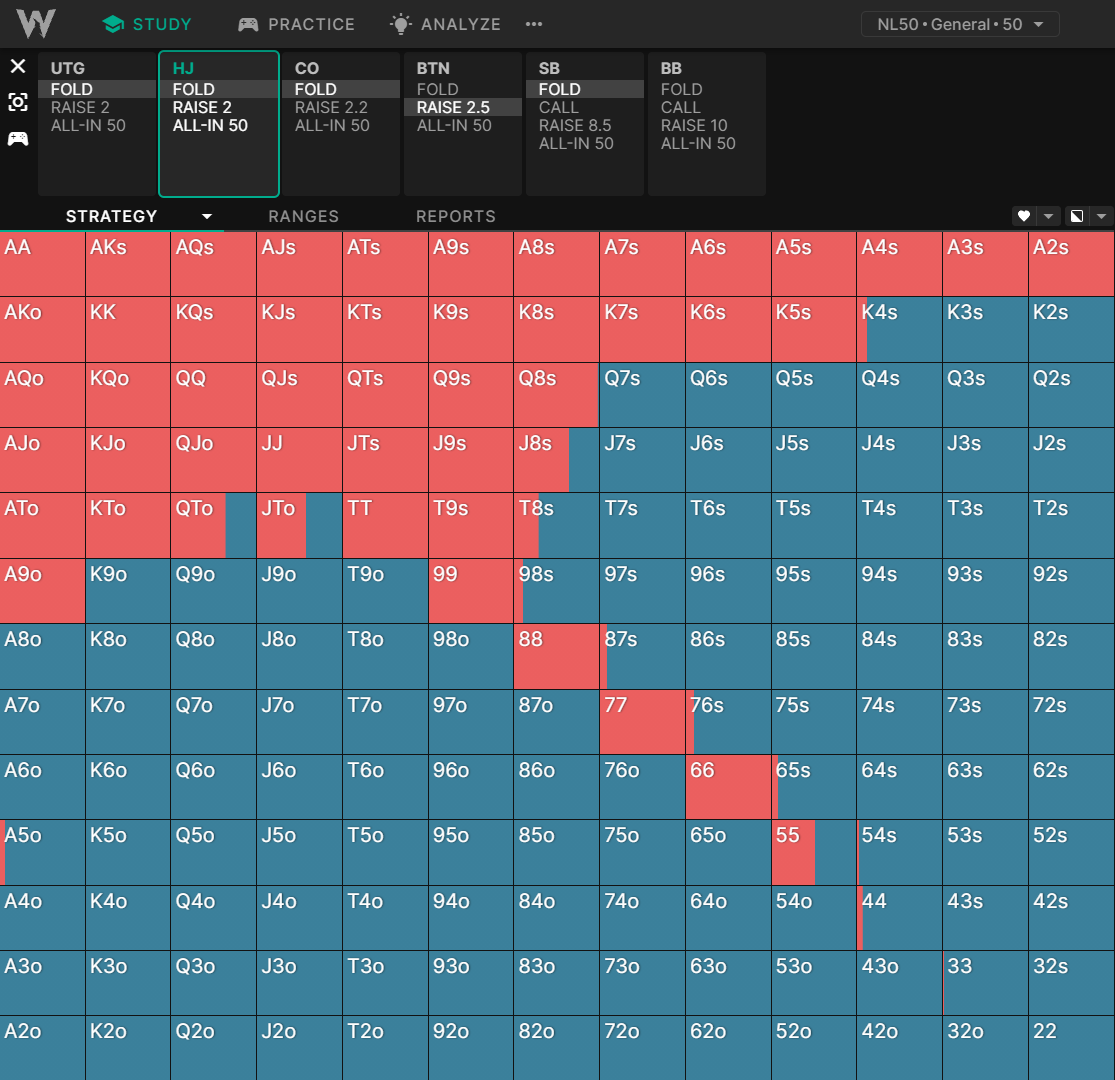
и®©жҲ‘们жҜ”иҫғдёҖдёӢеңЁж ҮеҮҶзҺ°йҮ‘жёёжҲҸдёӯпјҢжұӮи§ЈеҷЁеҰӮдҪ•еңЁдёҚеҗҢзҡ„зӯ№з Ғж·ұеәҰдёӢжү“ејҖ HJпјҡ
HJ ејҖзӣҳд»·пјҡ50BB ж·ұ
дҪ иҝҳеә”иҜҘиҖғиҷ‘еҜ№жүӢеңЁеҗҺз»ӯеӣһеҗҲжҠ•е…Ҙзӯ№з Ғзҡ„еҸҜиғҪжҖ§гҖӮдҫӢеҰӮпјҢеҰӮжһңдҪ зҡ„еҗҢиҠұеҗ¬зүҢеңЁжүҖжңүиғҪз»„жҲҗеҗҢиҠұзҡ„зүҢеһӢдёӯйғҪж— жі•жҲҗзүҢпјҢйӮЈд№ҲдҪ зҡ„еҗҢиҠұеҗ¬зүҢзҡ„йҡҗеҗ«иө”зҺҮе°ұдјҡйҷҚдҪҺгҖӮ
HJ ејҖеұҖпјҡ100BB ж·ұ
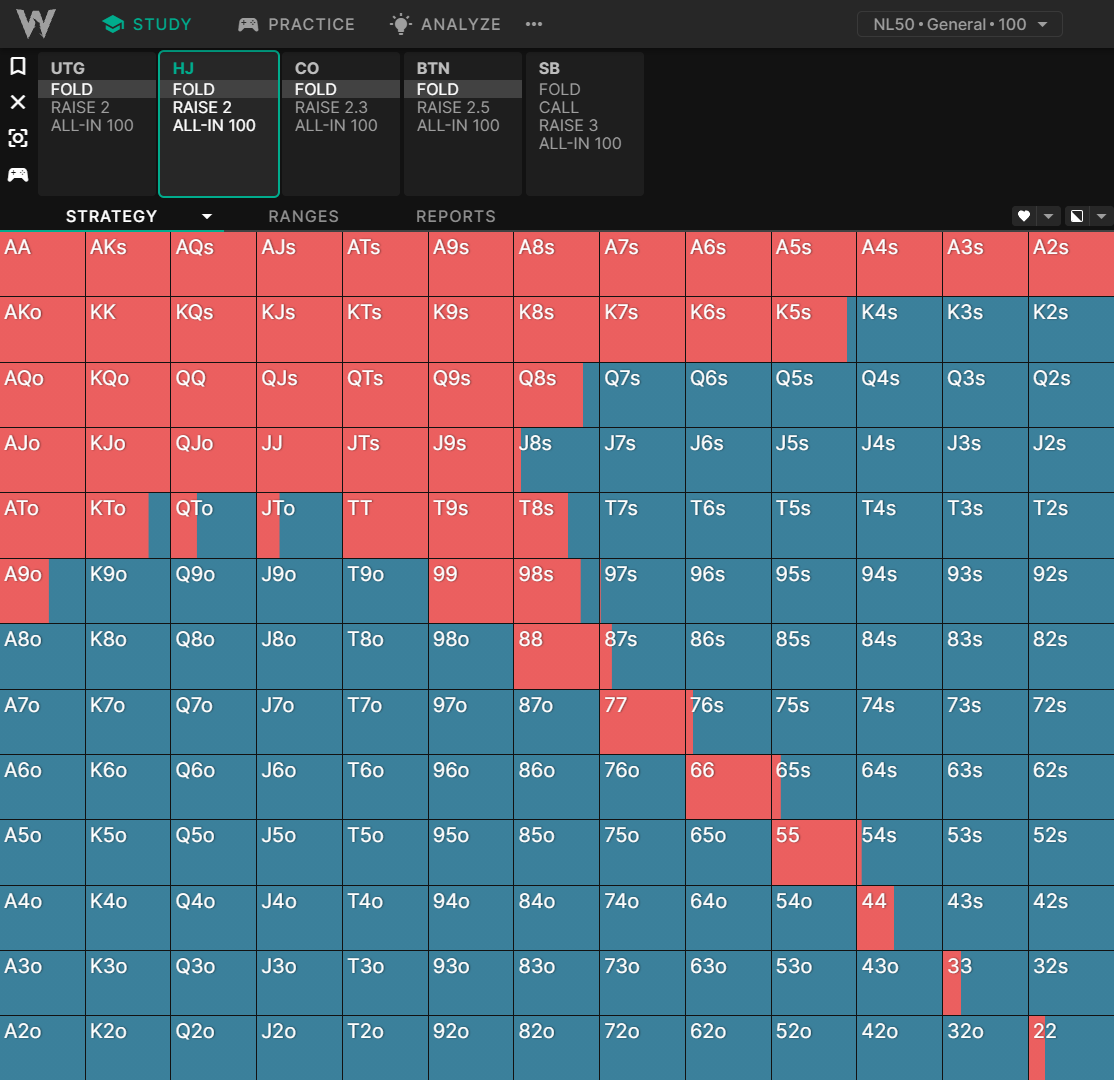
йҡҸзқҖеҲҶжһҗзҡ„ж·ұе…ҘпјҢжҲ‘们еҸ‘зҺ°зҺ©е®¶жӣҙеҖҫеҗ‘дәҺйҖүжӢ©дҪҺеҜ№еӯҗгҖҒеҗҢиҠұиҝһзүҢзӯүйҡҗеҗ«иө”зҺҮжӣҙй«ҳзҡ„зүҢеһӢгҖӮиҝҷз§ҚеҪұе“ҚиҷҪ然з»Ҷеҫ®пјҢдҪҶеңЁй”Ұж ҮиөӣеӣҫиЎЁдёӯеҚҙжӣҙдёәжҳҺжҳҫпјҡ
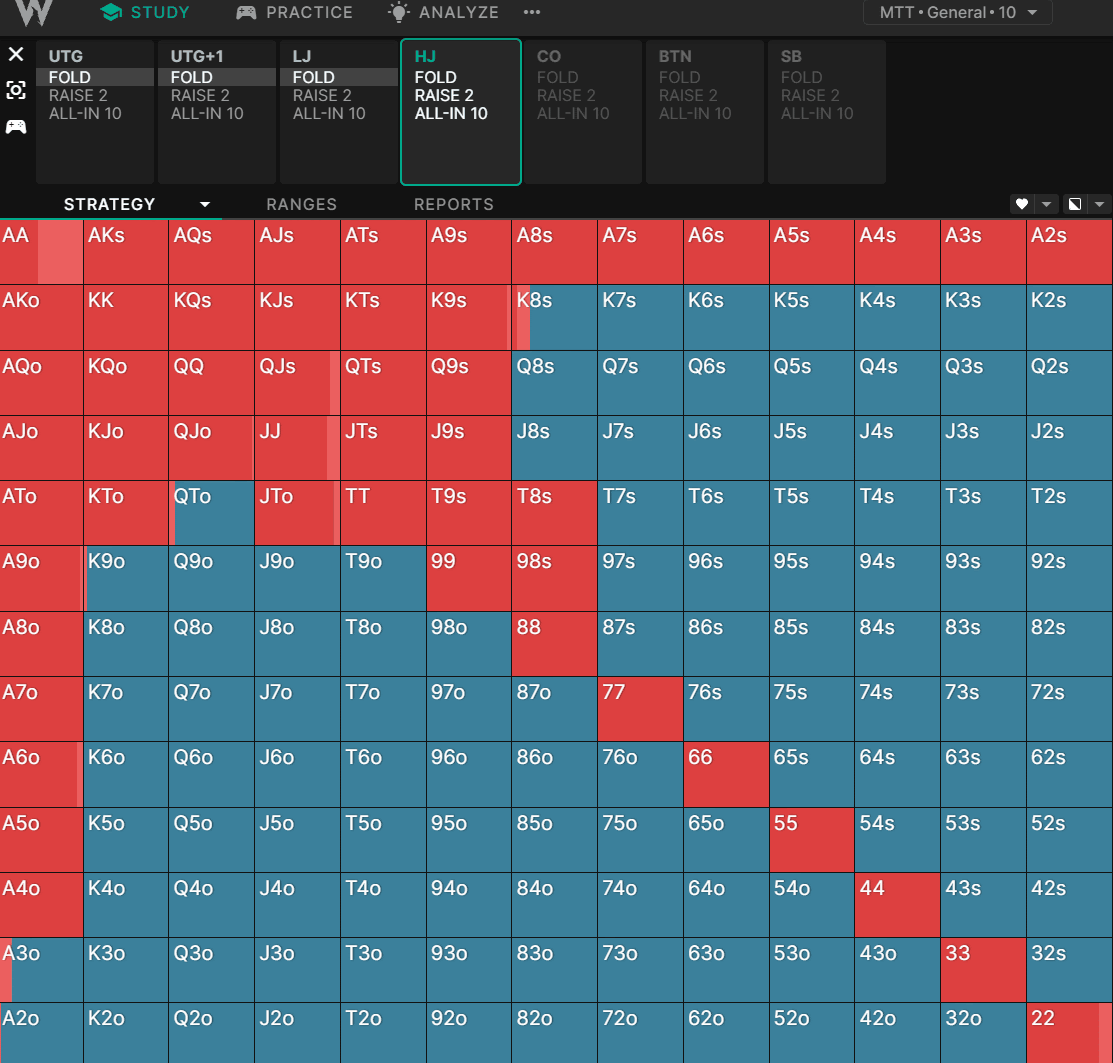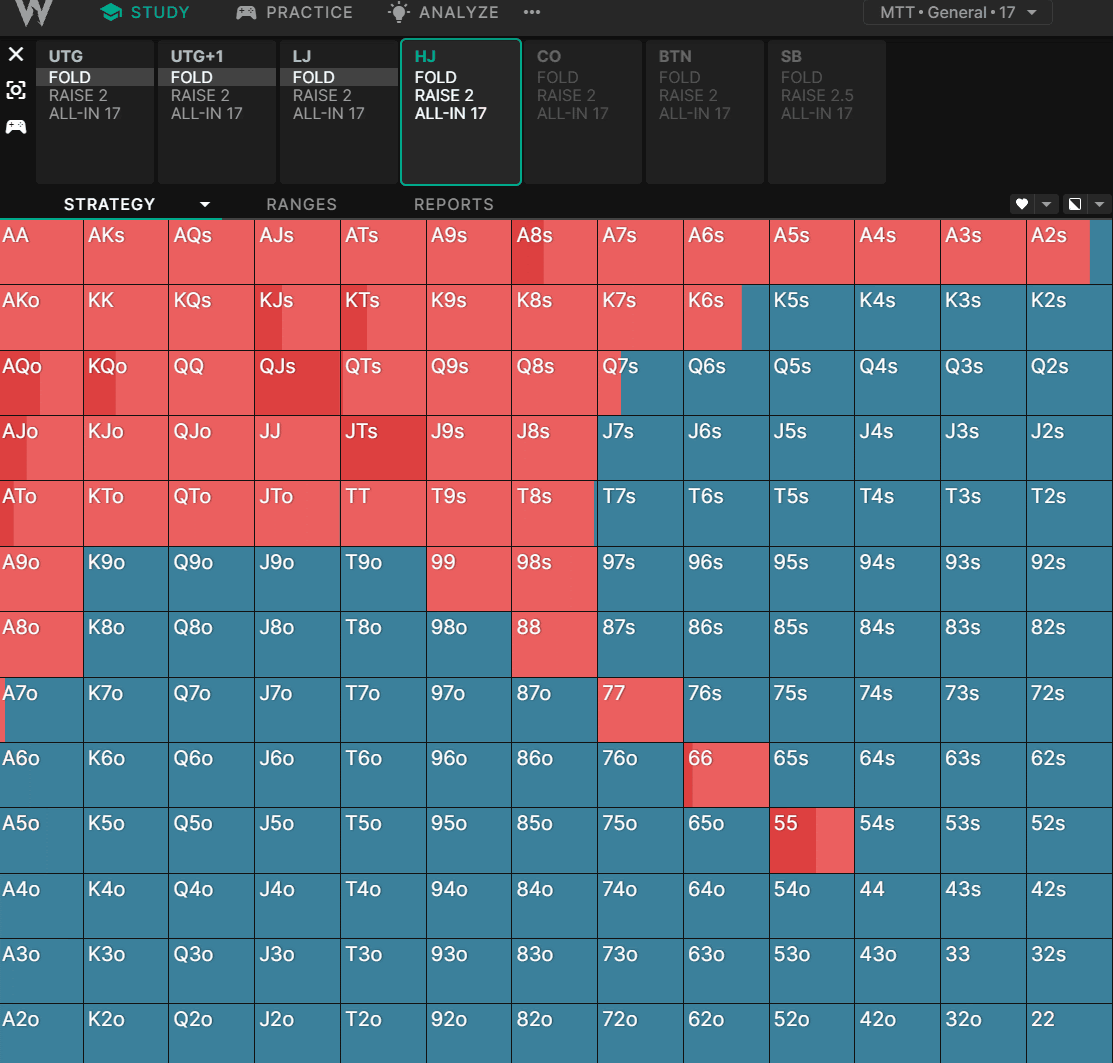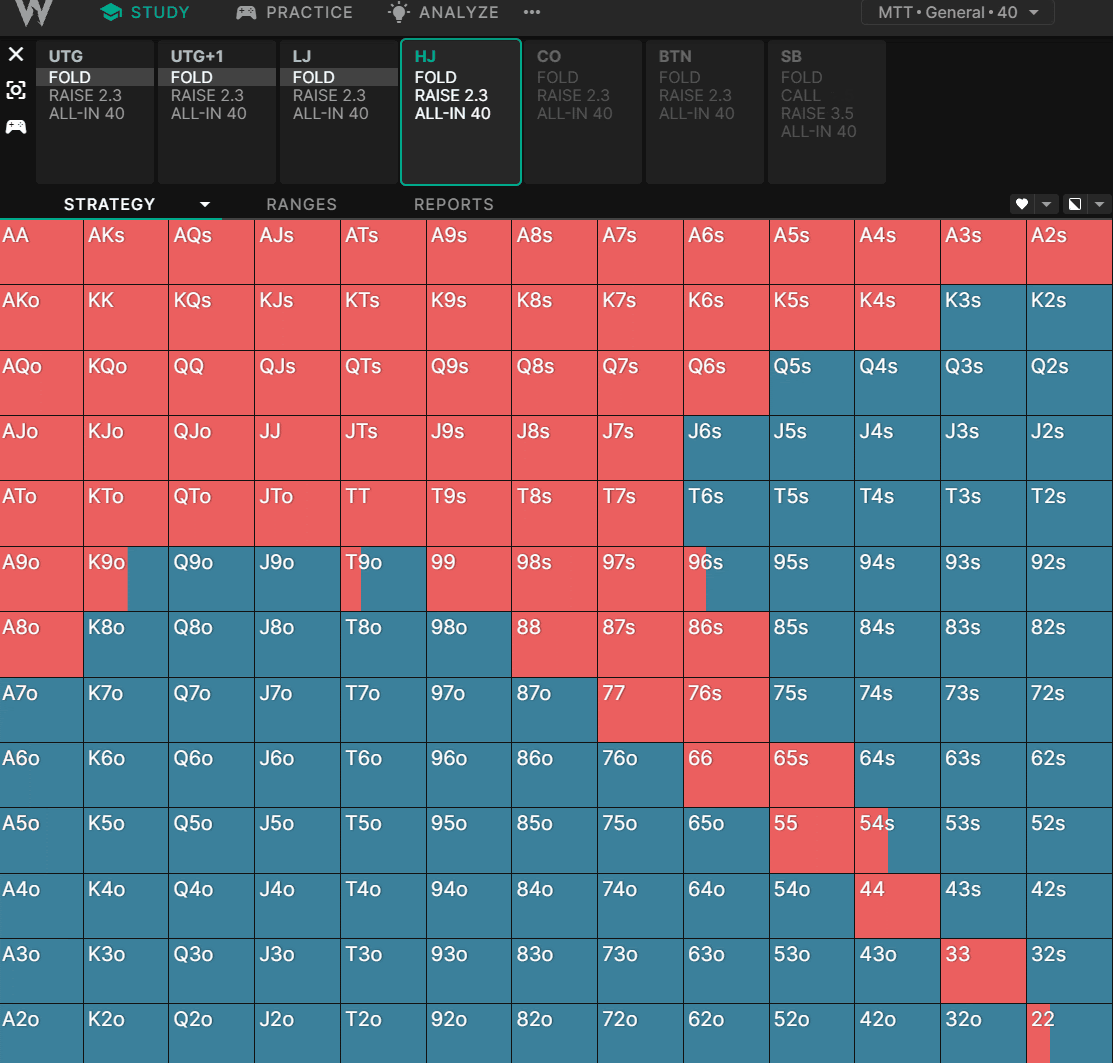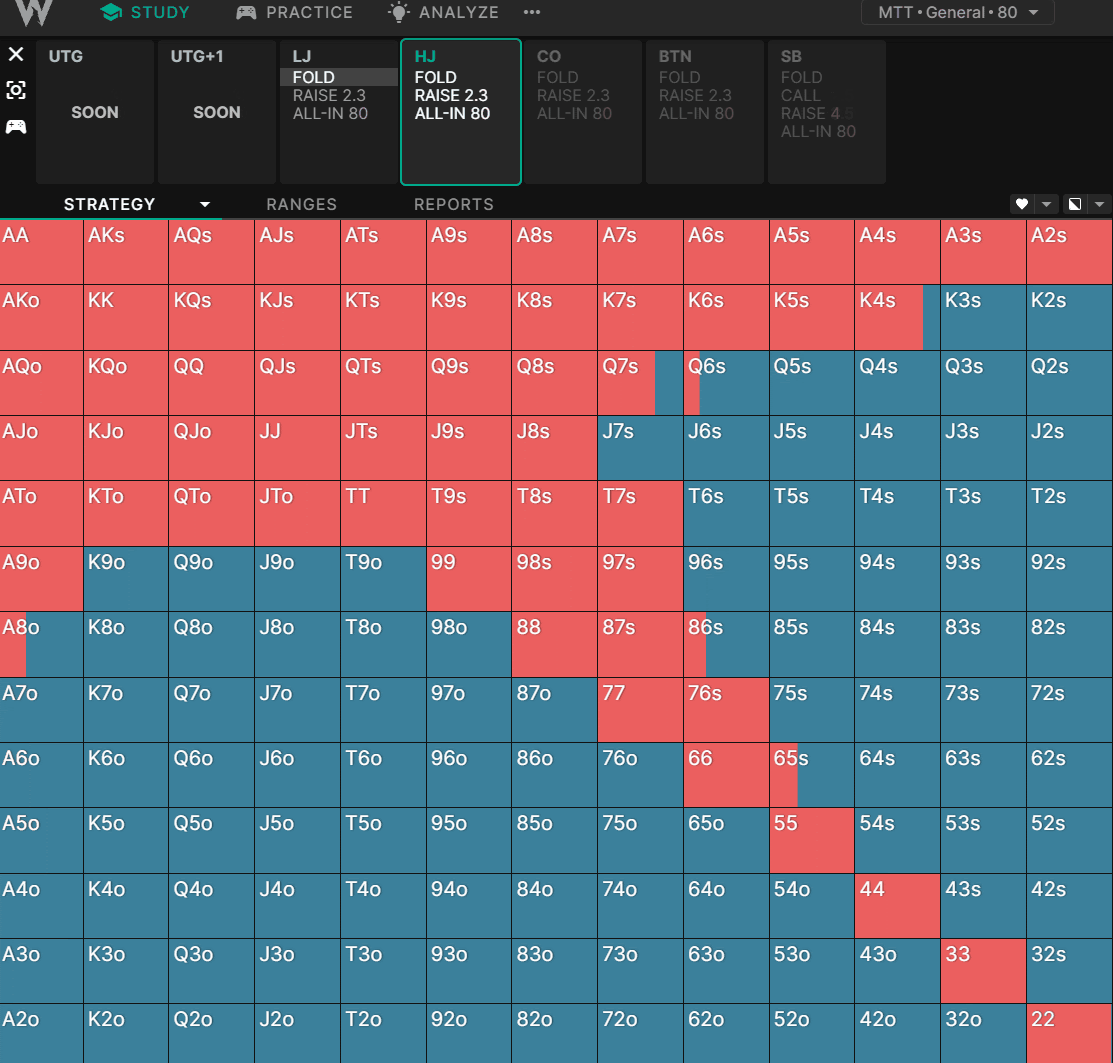
жҲ‘们еҸҜд»ҘзңӢеҲ°пјҢеңЁзӯ№з ҒйҮҸиҫғдҪҺж—¶пјҢзҺ©е®¶еҖҫеҗ‘дәҺйҖүжӢ©й«ҳиғңзҺҮзҡ„е…ЁжҠјпјҢиҖҢеңЁзӯ№з ҒйҮҸиҫғй«ҳж—¶пјҢеҲҷеҖҫеҗ‘дәҺйҖүжӢ©йҡҗеҗ«иө”зҺҮжӣҙй«ҳзҡ„вҖңеҸҜзҺ©вҖқзүҢеһӢгҖӮеҪ“зӯ№з ҒйҮҸиҫҫеҲ°60BBд»ҘдёҠж—¶пјҢз”ұдәҺйҡҗеҗ«иө”зҺҮзҡ„жҸҗй«ҳпјҢе…¶д»–зҺ©е®¶еҸҜд»Ҙз”Ёжӣҙе®Ҫзҡ„иҢғеӣҙе…ҘеұҖпјҢжӯӨж—¶зҺ©е®¶зҡ„иҢғеӣҙдјҡзј©е°ҸгҖӮ
йҖҡиҝҮеӨҡж–№жқғзӣҠдҝқз•ҷеҸҜи§ҶеҢ–йҡҗеҗ«иө”зҺҮ
йҡҗеҗ«иө”зҺҮдёҺдёҖжүӢзүҢз»„жҲҗжңҖејәзүҢеһӢпјҲnutbпјүзҡ„иғҪеҠӣзӣёе…ігҖӮжҲ‘们жңүж—¶з§°иҝҷз§Қж•Ҳеә”дёәвҖңеҸҜзҺ©жҖ§вҖқгҖӮд»ҘдёӢGIFеӣҫеұ•зӨәдәҶ2-14еҗҚзҺ©е®¶дҪҝз”Ёд»»ж„ҸдёӨеј зүҢж—¶зҡ„иө”зҺҮеҲҶеёғпјҢ并用йўңиүІиҝӣиЎҢдәҶзј–з ҒгҖӮеңЁиҝҷйҮҢпјҢжҲ‘们еҸҜд»ҘзңӢеҲ°иө”зҺҮеңЁеӨҡдәәжёёжҲҸдёӯжҳҜеҰӮдҪ•еҸҳеҢ–зҡ„гҖӮиҜ·жіЁж„Ҹиө”зҺҮзҡ„жёҗеҸҳпјҢиҖҢдёҚжҳҜе…·дҪ“зҡ„ж•°еҖјгҖӮ
д»ӨжҲ‘жғҠ讶зҡ„жҳҜпјҢжҲ‘еҸ‘зҺ°йҖҡиҝҮи°ғж•ҙзҺ©е®¶дәәж•°пјҲи°ғж•ҙйҡҗеҗ«иө”зҺҮзҡ„еҖјпјүпјҢеҸҜд»ҘеҲӣе»әеҮәдёҺGTOејҖеұҖиҢғеӣҙеӨ§иҮҙзӣёдјјзҡ„иғңзҺҮжўҜеәҰгҖӮдҫӢеҰӮпјҢдёӢеӣҫеұ•зӨәдәҶеүҚ44%зүҢеһӢзҡ„иғңзҺҮжўҜеәҰпјҢж—Ғиҫ№жҳҜж ҮеҮҶзҡ„100BBжҢүй’®дҪҚејҖеұҖиҢғеӣҙгҖӮ
иҮӘе·ұиҜ•иҜ•иҝҷдёӘз”өеӯҗиЎЁж јпјҒ
еҚідҪҝзүҢеұҖдёӯеҸӘеү©дёӢ3еҗҚзҺ©е®¶пјҢеңЁ100BBж·ұеәҰж—¶пјҢйҡҗеҗ«иө”зҺҮзҡ„д»·еҖјд№ҹдјҡиў«еӨёеӨ§гҖӮдёәдәҶжЁЎжӢҹGTOжңҹжңӣеҖјжўҜеәҰпјҢжҲ‘йҖҡиҝҮе°ҶеӨҡдәәзүҢеұҖзҡ„иғңзҺҮи®Ўз®—еўһеҠ еҲ°8еҗҚзҺ©е®¶пјҢдәәдёәең°жҸҗй«ҳдәҶйҡҗеҗ«иө”зҺҮгҖӮ
йҡҸзқҖзҺ©е®¶ж•°йҮҸзҡ„еўһеҠ пјҢиғңзҺҮжўҜеәҰеҗ‘жӣҙзӣёеҗҲгҖҒжӣҙиҝһиҙҜзҡ„зүҢеһӢеҖҫж–ңпјҢиҝҷдәӣзүҢеһӢжӣҙжңүеҸҜиғҪз»„жҲҗжңҖејәзҡ„зүҢеһӢгҖӮ
иҝҷж ·пјҢжҲ‘们е°ұжҠҠйҡҗеҗ«иө”зҺҮеҪ“дҪңдёҖдёӘеҸҜи°ғиҠӮзҡ„еҸӮж•°пјҢдәәдёәең°зӘҒеҮәдёҚеҗҢзұ»еһӢзүҢзҡ„еҶ…еңЁйҡҗеҗ«иө”зҺҮпјҲжҲ–иҖ…жӣҙеҮҶзЎ®ең°иҜҙпјҢжҳҜзүҢдёҺејәзүҢз»“еҗҲзҡ„еӣәжңүиғҪеҠӣпјүгҖӮ

еҚідҪҝзүҢеұҖеҸӘеү©дёӢ3еҗҚзҺ©е®¶пјҢеңЁ100BBж·ұеәҰж—¶пјҢйҡҗеҗ«иө”зҺҮзҡ„д»·еҖјд№ҹдјҡиў«еӨёеӨ§гҖӮдёәдәҶжЁЎжӢҹGTOжңҹжңӣеҖјжўҜеәҰпјҢжҲ‘дәәдёәең°е°ҶеӨҡдәәзүҢеұҖзҡ„иғңзҺҮи®Ўз®—еўһеҠ еҲ°8дәәпјҢд»ҺиҖҢжҸҗй«ҳдәҶйҡҗеҗ«иө”зҺҮгҖӮиҝҷз§ҚеҲҶжһҗж–№жі•дҪҺдј°дәҶйҳ»жҢЎж•Ҳеә”пјҢеӣ жӯӨжӣҙйҡҫжЁЎжӢҹж—©жңҹдҪҚзҪ®зҡ„ејҖеұҖиҢғеӣҙгҖӮж— и®әеҰӮдҪ•пјҢжҲ‘еёҢжңӣжӮЁе’ҢжҲ‘дёҖж ·е–ңж¬ўиҝҷдёӘйҡҗеҗ«иө”зҺҮзҡ„еҸҜи§ҶеҢ–е‘ҲзҺ°пјҒ



