二四法则和所罗门法则的简单运用与教程

一、二四法则和所罗门法则的简单介绍

德州扑克中的“二四法则”和“所罗门法则”都是用来计算成牌概率的，二者的计算规则如下：假设出牌（Outs）数量是X（基础分析不考虑对手的手牌和Redraw的情况，下同），则：

A、二四法则：

1条街的成牌概率约=X*2*1%；

2条街的成牌概率约=X*4*1%；

B、所罗门法则是对二四法则的修正，一条街的情况和二四法则没区别，两条街的时候当Outs数目大于或等于9的时候，要在二四法则基础上加一个修正项，为：

2条街的成牌概率约=(X*4-(X-8))*1%（由于录入方便性和网页演示问题，文中所有公式用Excel中公式格式展示）

举个例子：

翻牌抽同花Outs的数量=9，则用二四法则计算到河牌2条街的成牌概率=9*4*1%=36%；而用所罗门法则计算=(9*4-(9-8))*1%=35%——这里两个公式差异不大；

翻牌抽两头同花顺Outs的数量=15，则用二四法则计算到河牌2条街的成牌概率=15*4*1%=60%；而用所罗门法则计算=(15*4-(15-8))*1%=53%——这里两个公式差异就明显起来，所罗门法则明显更接近实际成牌概率。

二、进一步量化讨论二四法则和所罗门法则和实际成牌概率差异多大，适用的情况如何，将使用二四法则计算的成牌概率和实际概率差异用图表表示如下，其中两条街的实际成牌概率使用了高中数学中简单的排列组合知识：

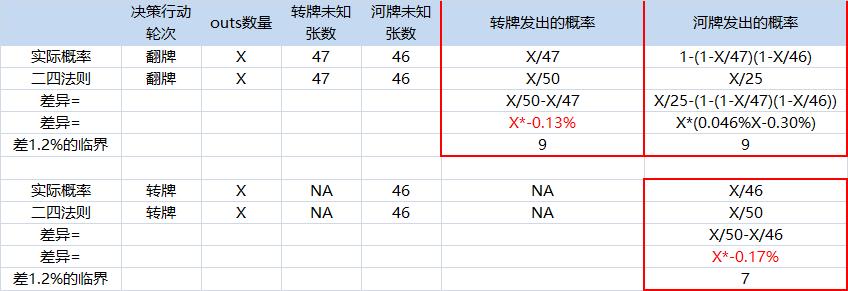
1、考虑一条街的情况下，二四法则计算成牌概率和实际的差异假设为Y，Y和Ous数量X是一阶线性关系，其中二四法则算出的概率会比实际概率小一点点。

翻牌未发出牌为47张：

Y=X*-0.13%，当Outs不大于9的时候，翻牌用二四法则计算下一条街成牌概率的与实际差异不超过1.2%；

转牌未发出牌为46张：Y=X*-0.17%，当Outs不大于7的时候，转牌用二四法则计算下一条街成牌概率的与实际差异不超过1.2%。

2、考虑两条街的情况下，二四法则计算成牌概率和实际的差异假设为Y，这时Y是Ous数量X的二阶函数，Y=X*(0.046%X-0.30%)，函数的图形是下图中的红色折线：

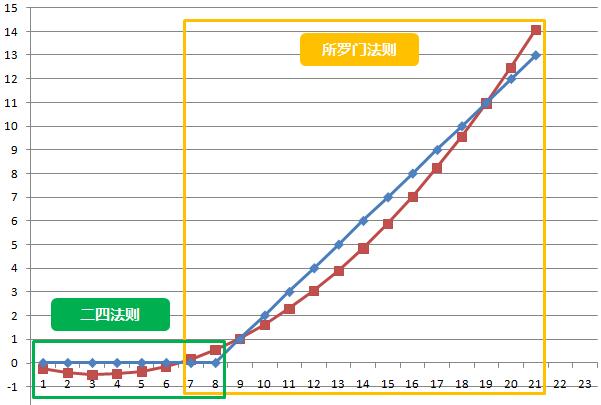
我们可以看出，上图中，当X大于等于1且小于等于8的时候，Y的绝对值不超过1.2%（实际不超过0.56%）；当X大于等于9的时候，函数Y随着X增大迅速增加。

那么我们怎么来解决二四法则公式当X大于等于9的时候差异过大的问题呢？这里就引入了所罗门法则所增加的修正项(X-8)*1%——当X大于等于9的时候，Y’=(X-8)*1%就是倾斜向上的蓝色折线这一段；

而Y-Y’的绝对值，即图中直观看红折线和蓝折线之间纵坐标差值，就是使用所罗门法则计算成牌概率和实际概率之间的差异。这个差异非常小，当X大于等于9，且小于等于21的时候，Y-Y’的绝对值不超过1.2%（实际不超过1.06%）而除了一些奇葩的场景，翻牌Outs=21基本可以看做抽牌一方Outs最多的场景了，比如花顺双抽两高张vs顶对=KsQs vs Jc8c @Flop=JsTs2h。因此我们可以看到所罗门法则在实际使用中覆盖面非常好。

三、总结

计算成牌概率时，当Outs数量在[1,8]区间的时候，我们使用二四法则；当Outs数量在[9,21]区间的时候，我们用所罗门法则。这样简化计算和实际的误差很小，通常不超过1.2%。